以下图为例:
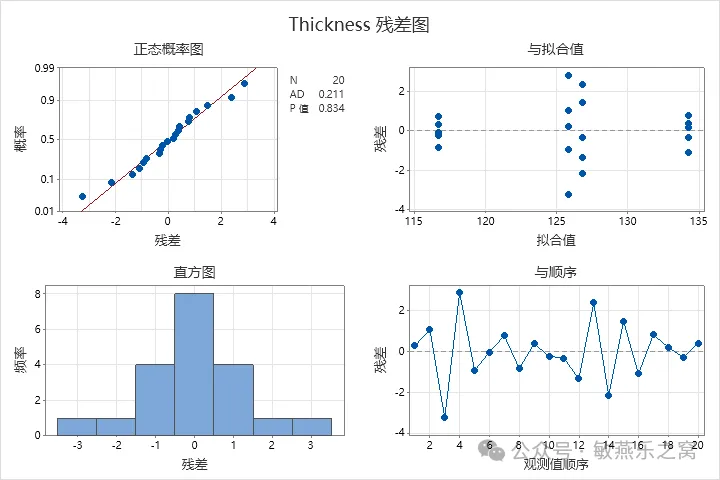
1)左上图
因为我们通常假设数据都是相互独立的,应符合N(f(x),σ^2)分布,因此残差作为响应变量数值与代入模型后的预测值之差,其分布也应该符合residual(残差)~(0,σ^2)。这时候我们通常根据左上图来判断,确认P值,如果大于0.05,则判断符合正态分布。如果小于0.05,说明模型可能不正确,需要对模型进行调整。
该图P值大于0.05,说明数据符合正态分布。
2)左下图
该柱状图也是配合左上图来确认残差是否符合正态分布,没有特别的意义。
3)右上图
该散点图重点确认该残差图是否保持等方差性,即是否有“漏斗形”或”喇叭形“。如果出现未等方差的现象,需要对响应变量y做出变换。
上图的散点图是正常的。
4)右下图
主要确认散点图的各点是否在无规则的波动,该图也是很容易出现问题的图表,如果残差保持了等方差,但是该图中有明显的U形或者倒U形的弯曲,说明应该增加X的平方项或者立方项。
四、残差值是否越小越好?
在统计分析中,通常情况下残差越小越好。这意味着实际观测值和模型预测值之间的差异越小,模型对数据的拟合程度就越好。在最小二乘法中,我们会尽量找到能够使残差平方和最小的拟合模型,以降低预测误差。
然而,有时候较大的残差也可能具有特殊的意义。例如,在异常值检测时,较大的残差可能表示存在离群点或者异常观测值。在这种情况下,较大的残差可以帮助我们识别可能存在的问题,需要进一步进行调查和分析。
因此,一般来说,我们希望残差尽可能地小,但对待残差的大小需要具体情况具体分析,不能一概而论。
这家伙很懒,还没有设置简介