正交实验的极差分析
-
-
呵呵呵 这家伙很懒，还没有设置简介
0 人点赞了该文章 · 848 浏览
正交实验的极差分析
3水平3因素正交实验方案设计：
当前有一项研究，研究大豆出油率分别与3个因素的关系情况，分别是萃取液，温度和处理时间。首先使用SPSSAU的正交设计得到正交表L9.3.4，总共进行9次试验收集完成试验数据后进行分析，希望找出3个因素时各水平的最佳大豆出油率组合
| 水平 | 萃取液 | 温度 | 处理时间 |
| 1 | 10 | 20度 | 1.5小时 |
| 2 | 50 | 35度 | 2.5小时 |
| 3 | 90 | 50度 | 3.5小时 |
另外，本案例数据如下表：表格中水平数量使用数字表格，比如因子2（温度）里面的数字1表示20度，数字2表示35度。
| 试验编号 | 因子1(萃取液量） | 因子2（温度） | 因子3（处理时间） | 大豆出油率（%） |
| 1 | 1 | 1 | 1 | 0 |
| 2 | 1 | 2 | 3 | 16 |
| 3 | 1 | 3 | 2 | 21 |
| 4 | 2 | 1 | 3 | 14 |
| 5 | 2 | 2 | 2 | 49 |
| 6 | 2 | 3 | 1 | 29 |
| 7 | 3 | 1 | 2 | 1 |
| 8 | 3 | 2 | 1 | 19 |
| 9 | 3 | 3 | 3 | 45 |
极差分析是一种直观式分析方法，一般我们希望先评价因素优劣，比如本案例中三个因素的优劣，评价标题是通过R值（因素极差值）进行评价；而具体水平的优劣可通过K avg值，即每个水平时试验数据的平均值，对于K avg值的大小即可得到水平优劣的对比。最终结合因素优劣和水平优劣，即可找出最佳试验组合。
极差分析时，涉及相关指标的计算说明如下：
K值：每因子每水平时 实验数据的相加和值
K avg值：每因子每水平时 实验数据的平均值
最佳水平：每因子时，K avg值最大时对应的水平
R：每因子时，K avg值的最大值 减去 K avg值的最小值
水平数量：每因子时的水平数量
每水平重复数r：每个水平平均实验次数
折算系数d：每因子时，水平数量对应的折算系数d值
极差分析
| 极差分析表格 | ||||
| 项 | 水平 | 因子1(萃取液量） | 因子2（温度） | 因子3（处理时间） |
| K值 | 1 | 37.00 | 15.00 | 48.00 |
| 2 | 92.00 | 84.00 | 71.00 | |
| 3 | 65.00 | 95.00 | 75.00 | |
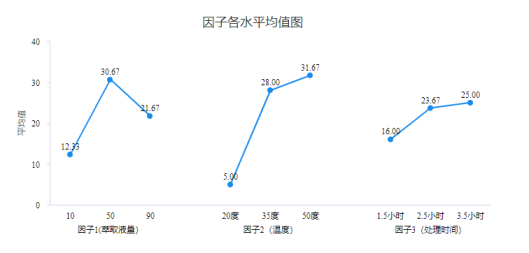
| K avg值 | 1 | 12.33 | 5.00 | 16.00 |
| 2 | 30.67 | 28.00 | 23.67 | |
| 3 | 21.67 | 31.67 | 25.00 | |
| 最佳水平 | 2 | 3 | 3 | |
| R | 18.34 | 26.67 | 9.00 | |
| 水平数量 | 3 | 3 | 3 | |
| 每水平重复数r | 3.0 | 3.0 | 3.0 | |
上表格为极差分析的结果，极差分析表格中可知：从3个因素来看，结合R值（因素极差值）的大小对比可知，因子2温度是最优因素，其次是因子1萃取液量，最后是因子3处理时间。因而3个因素的优劣排序为：因子2（温度）>因子1（萃取液量）>因子3（处理时间）。
具体结合各因子的最佳水平可知，因子1萃取液量时第2个水平即50时最优，因子2温度以第3个水平即50度最优，因子3处理时间以第3个水平即3.5小时最优。
综合上述分析可知：最优因子为温度。最优组合为“温度50度，萃取液量50，处理时间3.5小时”。
通过图形可直观查看如下：
全部 0条评论