设定一个硬币正反面的假设实验,这里假设检验的思路就是:
假设:硬币是公平的
检验:认为假设是成立的,然后扔十次,看结果与假设是否相符
反复扔硬币应该符合二项分布(这就不解释了),也就是:

其中, 图片 代表扔硬币的次数, 图片 代表“花”朝上的概率。
在我们认为硬币是公平的前提下,扔10次硬币应该符合以下分布:
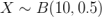
下图表示的就是,假如硬币是公平的情况下的分布图: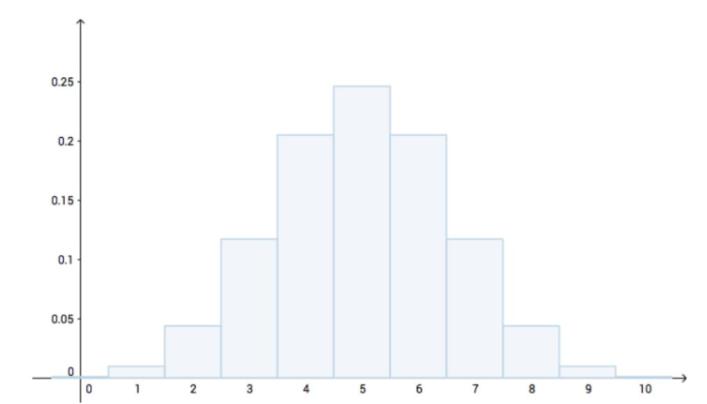
我扔了十次之后得到的结果是,有八次正面: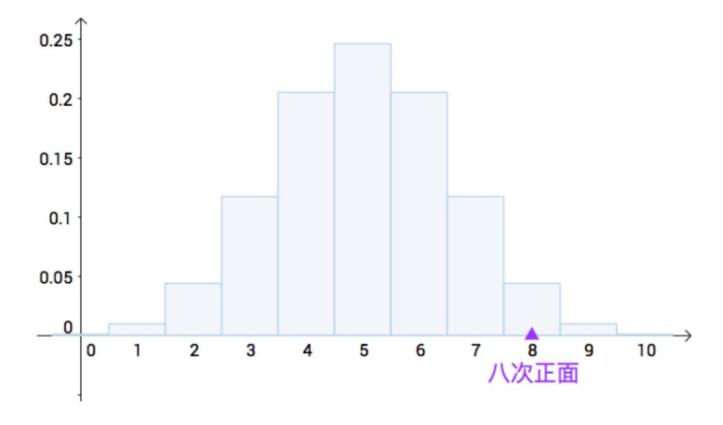
这个时候有个数学大佬就出来定义了一个称为 图片 值(p-value)的概念: 罗纳德·艾尔默·费希尔爵士(1890-1962)。
罗纳德·艾尔默·费希尔爵士(1890-1962)。
把八次正面的概率,与更极端的九次正面、十次正面的概率加起来:
得到的就是(单侧P值):
其实,出现两次正面、一次正面、零次正面的概率也是很极端的:
所以(双侧P值): 2.1 为什么要把更极端的情况加起来?
2.1 为什么要把更极端的情况加起来?
根据扔硬币这个例子,可能你会觉得,我知道八次正面出现不正常就行了,干嘛要把九次、十次加起来?
我觉得有这么一个现实原因,比如我要扔1000次硬币来测试假设是否正确。
扔1000次硬币用二项分布来计算很麻烦,根据中心极限定理,我们知道,可以用正态分布来近似:
比如,我扔了1000次,得到了530次正面,用正态分布来计算就比较简单。
但是,对于正态分布,我没有办法算单点的概率(连续分布单点概率为0),我只能取一个区间来算极限,所以就取530、以及更极端的点组成的区间:
我上面只取了单侧P值,说明下:
取单侧还是双侧,取决于你的应用
什么叫做更极端的点,也取决于你的应用
3 显著水平
总共扔10次硬币,那么是出现7次正面之后,可以认为“硬币是不公平的”,还是9次正面之后我才能确认“硬币是不公平的”,这是一个较为主观的标准。
我们一般认为
就可以认为假设是不正确的。
0.05这个标准就是显著水平,当然选择多少作为显著水平也是主观的。
比如,上面的扔硬币的例子,如果取单侧P值,那么根据我们的计算,如果扔10次出现9次正面:
表示出来如下图所示:
我们可以认为刚开始的假设错的很“显著”,也就是“硬币是不公平的”。
如果扔10次出现出现8次正面:
呃,这个和我们的显著水平是一样的啊,我们也可以拒绝假设,只是没有那么“显著”了。