SPC理论都是基于正态分布来定义判异的,非正态分布很明显不适应的。
非正态数据直接做SPC控制图
对于下面这样的一组检测数据,我们直接做SPC控制图。
286,948,536,124,816,729,4,143,431,8,2837,596,81,227,603,492,1199,1214,2831,96


按照SPC八大判异规则,可以看到有几个点的异常。(注:SPC分析的判异是基于正态分布的,所以上面的异常并不一定准确)
SPC就是制定一些规则,这些规则在正常情况下(正态分布),发生的概率很低(低于5%),如果发生了,我们就认为是异常。
我们先看看这组数据是否符合正态分布,先做一个正态概率纸,可以看到这些点不在同一条直线附近,很明显不符合正态分布。

我们用量化来判断一下是否是正态分布。

四种正态性检验的方法算出来的P值都远远小于0.05,很明显不符合正态分布。(SPC分析中最常用的是Anderson-Darling Test,简称AD检验)。
所以,上面的控制图是不能这样做的。
做正态性变换后做SPC控制图
在统计过程控制中,尤其是当数据明显偏离正态分布时,应该使用Box-Cox变换后,再编制SPC控制图,这样才更有助于减少误报和遗漏报,提高过程控制的整体效率。
Box-Cox 变换的目的是将非正态分布数据转换成近似正态分布。这个变换定义为:



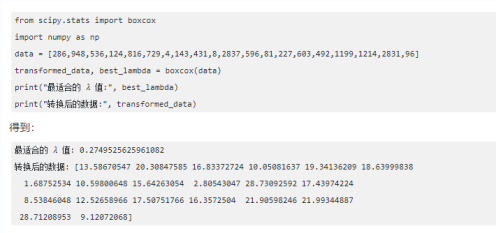
对转换后的数据做正态性分析:


用转换后的数据做SPC控制图:


可以看到,经过正态性转换的数据编制的SPC控制图,可以看到我们的过程是在受控状态,不存在异常因素的影响。
变换后的作用
正态性改善:使数据更符合正态分布的假设,这对于许多统计测试和控制图的效力至关重要。
方差稳定性:Box-Cox变换有助于稳定方差,这对于统计过程控制中的监控非常重要,因为许多控制图假设过程方差恒定。
这家伙很懒,还没有设置简介